布隆过滤器算法原理,高效概率型数据结构原理与应用

想象你正在设计一个系统，需要高效地判断一个元素是否存在于庞大的数据集中。传统的数据结构如哈希表或树结构，在数据量巨大时，查询效率会显著下降，内存占用也居高不下。这时，布隆过滤器算法原理如同一道曙光，为解决这一难题带来了创新的思路。布隆过滤器，这个由美国计算机科学家Burton Howard Bloom在1970年提出的概率型数据结构，以其独特的空间效率和查询速度，成为了许多现代系统中不可或缺的一部分。今天，就让我们一起深入探索布隆过滤器的奥秘，看看它是如何通过巧妙的设计，在保证高效查询的同时，又引入了不可避免的假阳性概率。

布隆过滤器的核心构造

布隆过滤器的核心构造非常简单，主要由一个很长的二进制向量和一系列哈希函数组成。这个二进制向量，也称为位数组，初始时所有位都设置为0。哈希函数的数量通常为k，这些函数负责将数据映射到位数组的特定位置上。当你想要添加一个元素时，布隆过滤器会通过k个哈希函数计算出k个哈希值，并将这些值对应的位数组位置设为1。查询时，同样使用这k个哈希函数计算位置，如果所有对应的位置都是1，则该元素可能存在于集合中；如果有任何一个位置是0，则该元素一定不存在。

布隆过滤器的运作机制

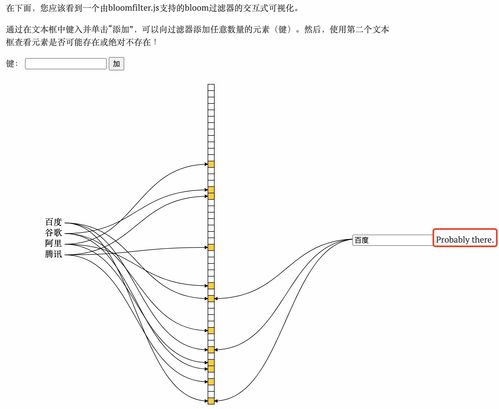
布隆过滤器的运作机制基于哈希函数的映射和位数组的更新。以一个包含3个哈希函数的布隆过滤器为例，假设我们要添加元素X。首先，通过3个哈希函数分别计算出3个哈希值，比如1、4、8。将位数组中对应这些哈希值的位置设为1。接下来，如果我们要查询元素X是否存在于集合中，同样使用这3个哈希函数计算出哈希值，并检查位数组中对应位置是否都为1。如果都为1，则元素X可能存在；如果任何一个位置为0，则元素X一定不存在。

假阳性与误判率

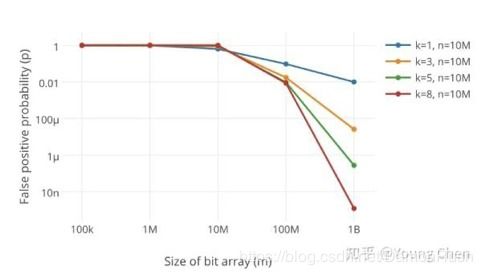
布隆过滤器的一个主要缺点是存在假阳性的可能性。由于哈希函数的碰撞，多个不同的元素可能会映射到位数组的相同位置，导致误判。例如，如果元素Y通过哈希函数映射到了与元素X相同的位数组位置，那么在查询元素X时，可能会错误地认为元素X存在。这种假阳性的概率与位数组的长度m、哈希函数的个数k以及布隆过滤器中存入的数据量n有关。当m增大、k增大、n减小时，假阳性率会降低。因此，在设计布隆过滤器时，需要综合考虑这些因素，以达到最佳的性能平衡。

布隆过滤器的应用场景

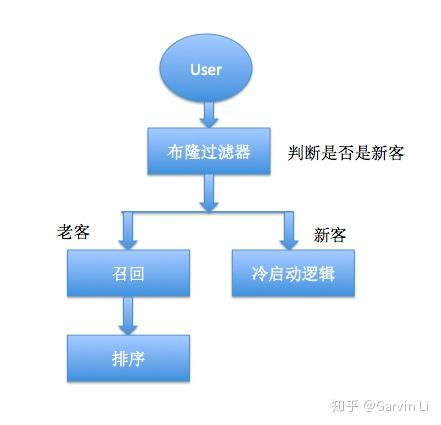
布隆过滤器的应用场景非常广泛。在网络系统中，它可以用于缓存穿透，防止恶意请求穿透缓存直接访问数据库。在集合重复检测中，例如在大数据场景中，可以快速检测一个元素是否已经在集合中。在网络系统中的数据包检测方面，如检测一个数据包是否已经发送过。此外，布隆过滤器还可以用于反垃圾邮件系统，判断某个电子邮件是否曾被标记为垃圾邮件，以及Web爬虫，判断URL是否已经被爬取，避免重复爬取相同的页面。

布隆过滤器的优势与挑战

布隆过滤器的优势在于其空间效率和查询速度。相比于传统的数据结构，布隆过滤器在存储空间和查询时间上都有很大的优势。它不需要存储元素本身，只存储元素是否存在的信息，这对于对保密要求严格的场合有优势。布隆过滤器也存在一些挑战。首先，它不能提供100%准确的判断，存在误报的可能性。其次，布隆过滤器不支持删除操作，因为删除一个元素可能会导致其他元素的哈希值映射到同一个位置，从而影响查询结果。为了解决这个问题，一些系统会建立一个小的白名单，存储那些可能被误判的元素，以减少误报的影响。

通过深入理解布隆过滤器的原理和应用，我们可以看到它在现代系统中的重要作用。虽然布隆过滤器存在一些局限性，但其高效的空间利用和查询速度使其成为处理大规模数据集时的理想选择。随着技术的不断发展，布隆过滤器将会在更多领域发挥其独特的优势，为我们的生活带来更多便利。