布隆过滤器怎么误判,布隆过滤器误判原理与应对策略解析

想象你正在开发一个高效的缓存系统，希望避免那些查询不存在的数据而频繁访问数据库的情况。这时，布隆过滤器这个神奇的数据结构就闪亮登场了。它就像一个高效的过滤器，能快速告诉你某个元素是否可能存在于集合中。但别急，布隆过滤器虽然强大，却也有它的“小脾气”——误判。那么，布隆过滤器究竟是怎么误判的呢？让我们一起揭开这个谜团。

布隆过滤器的原理

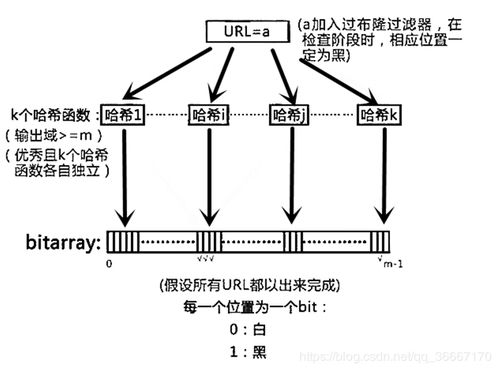
布隆过滤器是一种概率型数据结构，它通过位数组和多个哈希函数来实现快速判断元素是否存在。位数组就像一个巨大的开关，每个位初始时都是关闭的（值为0）。当你向布隆过滤器中添加一个元素时，多个哈希函数会分别对元素进行计算，得到多个不同的位数组索引。这些索引对应的位会被设置为开启状态（值为1）。查询时，同样通过这些哈希函数计算索引，如果所有对应的位都是开启的，就认为元素可能存在；如果任意一个位是关闭的，则元素一定不存在。

误判的根源

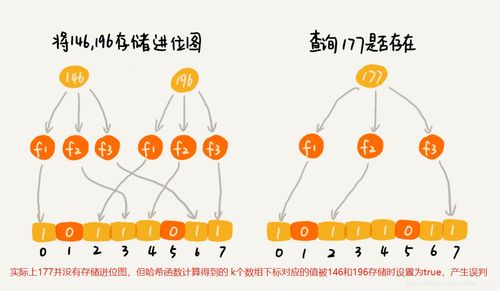
布隆过滤器的误判主要源于两个方面：哈希冲突和不可逆性。

哈希冲突

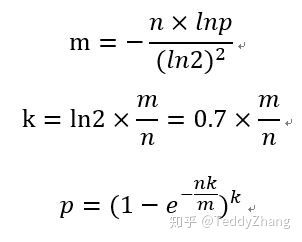
哈希函数将元素映射到位数组的位置时，可能会出现不同的元素映射到同一个位置的情况，这就是哈希冲突。随着插入到布隆过滤器中的元素数量增加，哈希冲突的概率也会增加。假设你有一个布隆过滤器，位数组大小为1000，使用3个哈希函数。当你插入100个元素后，每个元素通过3个哈希函数计算出的位数组索引会被设置为1。如果这些元素之间发生哈希冲突，位数组中的一些位可能会被多次设置为1，导致误判。

不可逆性

布隆过滤器一旦将某个位置的位设置为1，就不会再改回0。这意味着即使后来发现某些位是因为其他元素的存在而被错误地标记为1，也无法纠正这种状态。这种不可逆性增加了误判的可能性。比如，某个元素A通过哈希函数计算出的位数组索引对应的位已经被其他元素设置为1，当你查询元素A时，布隆过滤器会误判元素A存在。

误判率分析

误判率是布隆过滤器的一个重要参数，通常用假阳性率（False Positive Rate）来衡量。假阳性率指的是在过滤器中查询一个不存在的元素时，会将其误认为存在的概率。误判率取决于哈希函数的数量、被过滤的元素数量和过滤器的大小。

假设你有一个布隆过滤器，位数组大小为m，使用k个哈希函数，已经插入了n个元素。误判率可以通过以下公式计算：

\\[ p = (1 - e^{-kn/m})^k \\]

这个公式告诉我们，增加位数组的大小m或增加哈希函数的数量k都可以降低误判率。但需要注意的是，增加位数组的大小会增加存储成本，增加哈希函数的数量会增加计算开销。因此，在实际应用中，需要在误判率和空间效率之间做出权衡。

控制误判率的策略

为了控制布隆过滤器的误判率，可以采取以下策略：

增加位数组的大小

增加位数组的大小可以减少哈希冲突的概率，从而降低误判率。但位数组越大，占用的存储空间也越多。因此，需要根据实际需求选择合适的位数组大小。

增加哈希函数的数量

增加哈希函数的数量可以提高误判率的控制能力。但哈希函数越多，计算开销也越大。因此，需要平衡哈希函数的数量和计算效率。

定期更新布隆过滤器

随着业务数据的变化，布隆过滤器中的元素集合也会改变。定期重建布隆过滤器，能使它更准确地反映当前的数据集合，减少误判的可能性。比如，每天凌晨业务低谷期，重新计算布隆过滤器的位数组和哈希函数。

误判的影响及应对

布隆过滤器的误判虽然不可避免，但通常不会对业务造成严重影响。不过，在某些场景下，误判可能会带来一些问题。以下是一些常见场景及应对措施：

缓存穿透场景

在缓存系统中，误判可能导致原本不存在的数据也会去查询数据库，增加数据库的压力。应对措施是采用回源查询的方式，当布隆过滤器误判时，虽然会多一次数据库查询，但能确保不会将大量无效请求发送到数据库。同时，可以对数据库查询进行限流和熔断处理，避免数据库被压垮。

数据去重场景

在数据去重场景中，误判可能使某些重复数据被认为是新数据，从而影响去重的准确性。应对措施是结合其他精确的去重方法，如哈希表。先使用布隆过滤器进行初步过滤，再用哈希表进行精确去重。

访问控制

在访问控制场景中