布隆过滤器有什么用,高效数据存在性检测与大数据场景下的空间优化利器

你有没有想过，在浩瀚的数据海洋中，如何快速判断一个元素是否存在于某个集合里？传统的数据结构，比如哈希表、树或者链表，虽然功能强大，但当面对海量数据时，它们的缺点也暴露无遗——内存占用大，查询速度受数据规模影响。这时候，一个神奇的数据结构——布隆过滤器，就闪亮登场了。它就像一个高效的过滤器，能够以极小的代价告诉你，某个元素“可能在”集合中，或者“一定不在”集合中。今天，就让我们一起探索布隆过滤器的奥秘，看看它在实际应用中究竟有什么用。

布隆过滤器的核心原理

布隆过滤器由一个长度为m的二进制位数组和k个哈希函数组成。它的核心思想是，当一个元素被加入集合时，通过k个哈希函数计算出k个位置，并将这些位置的值设为1。查询时，同样用k个哈希函数计算位置，如果所有位置的值均为1，则认为元素可能存在；否则一定不存在。

想象你有一个巨大的图书馆，你想快速知道某本书是否在里面。布隆过滤器就像一个超级图书管理员，它不会告诉你书的具体位置，但能告诉你这本书“可能存在”或者“一定不存在”。这种判断的依据是，每个书架上的标记都被多个不同的哈希函数处理过，如果某个书架的标记都是1，那么这本书很可能就在那里；如果有一个标记是0，那么这本书一定不在。

布隆过滤器的优点

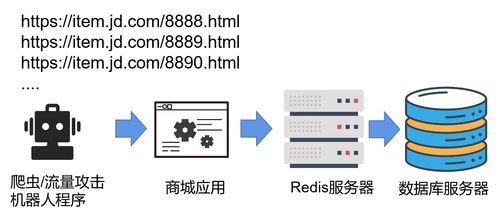
布隆过滤器的最大优点在于它的空间效率和查询速度。相比传统的数据结构，它占用的内存极小，而且插入和查询的时间复杂度都是O(k)，与数据规模无关。这意味着，无论你的数据集有多大，布隆过滤器的性能都不会下降。

以网络爬虫为例，假设你想要爬取整个互联网上的网页，但又不希望重复爬取相同的网页。这时候，布隆过滤器就能派上用场了。你只需要将每个爬取到的URL通过k个哈希函数映射到位数组中，并标记为1。当再次遇到一个URL时，只需进行同样的哈希计算，如果所有对应位置的值都是1，就说明这个URL已经爬取过了，可以跳过；否则，就继续爬取。

布隆过滤器的缺点

当然，布隆过滤器也不是完美的。它的最大缺点是存在误判的可能性，即可能会误判一个不存在的元素为存在。但不会误判一个存在的元素为不存在。这种误判的概率与位数组的大小m、哈希函数的个数k以及数据规模n有关。通过合理选择m和k的值，可以降低误判率。

此外，布隆过滤器不支持直接删除元素。因为删除操作可能会影响其他元素的判断。不过，有一些改进的布隆过滤器，比如计数布隆过滤器，支持元素的删除，但它们通常需要更多的空间和计算资源。

布隆过滤器的应用场景

布隆过滤器在现实世界中有广泛的应用，尤其是在需要快速判断元素是否存在的场景中。以下是一些典型的应用场景：

1. 缓存系统：在缓存系统中，布隆过滤器可以快速判断一个请求是否已经缓存。如果请求对应的布隆过滤器标记为1，就说明可能已经缓存了，可以直接返回结果，避免不必要的数据库查询。这样可以大大减轻数据库的负担，提高系统的响应速度。

2. 垃圾邮件过滤：布隆过滤器可以用来快速判断邮件地址或内容是否属于垃圾邮件库。如果某个邮件地址或内容的布隆过滤器标记为1，就说明可能已经是垃圾邮件了，可以直接过滤掉，避免浪费时间和资源。

3. 分布式系统：在分布式系统中，布隆过滤器可以用来判断数据是否已处理。例如，在分布式数据库中，每个节点可以使用布隆过滤器来标记已经处理过的数据，避免重复处理。

4. 区块链与分布式存储：在比特币等区块链技术中，轻节点可以使用布隆过滤器来验证交易是否存在，从而减少对完整节点的依赖，提高效率。

如何选择合适的布隆过滤器参数

布隆过滤器的性能很大程度上取决于参数的选择。位数组的大小m和哈希函数的个数k是两个关键参数。选择合适的m和k，可以在空间效率和误判率之间找到平衡点。

一般来说，m和k的选择需要根据实际应用场景来决定。例如，如果你对误判率要求较高，可以选择较大的m和k值；如果你对空间效率要求较高，可以选择较小的m和k值。此外，还可以通过实验来找到最佳的m和k值，以适应你的具体需求。

布隆过滤器的未来展望

随着大数据时代的到来，数据量不断增长，对数据处理的效率要求也越来越高。布隆过滤器作为一种高效的概率型数据结构，将在未来发挥更大的作用。随着技术的不断发展，布隆过滤器的